From Models to Mitigation: The Role of HPC in Infectious Diseases Modelling

During the COVID-19 pandemic, several measures were taken to reduce the spread of the disease, including lockdowns, vaccination campaigns, and compulsory masks in certain areas. However, the arrival of new variants and the unpopularity of coercive methods limited the effectiveness of these strategies. To prevent future major public health crises, it is essential to understand the efficacy of each measure for different population subgroups. In this way, Belgian scientists analysed data from the different phases of the epidemic and developed a mathematical model to conduct scenario analyses and better understand the transmission dynamics, thereby allowing for an assessment of the impact of interventions on future COVID-19 waves and, in the longer term, other potential outbreaks.

A National and European-Scale Project

Nicolas Herman is a young postdoctoral researcher working with Professor Nicolas Franco at the Namur Institute for Complex Systems (NaXys) of the University of Namur. Steven Abrams is a tenure track assistant professor at the University of Hasselt, together with Prof. Niel Hens. They are all part of the national Modeling Consortium which also includes Sciensano, with a focus on modelling infectious disease dynamics in the Belgian population. They were also actively involved in activities of the European Covid-19 Scenario Hub established by the European Centre for Disease Control and Prevention (ECDC). Prof. Franco’s team is also now part of the SIMID (SImulation Models of Infectious Disease) group, started in 2006 as a result of an interuniversity project between UHasselt and the University of Antwerp in Flanders, long before SARS-CoV-2 emerged. Since the pandemic began, the SIMID group has published many open-access papers, technical reports, and popularized articles for the general public, detailing the results obtained with their model.

Putting People into Boxes

Steven Abrams: “Formulating a mathematical model always entails a simplification of reality in order to translate the complex interactions between people that enable disease spread into a set of mathematical equations.”

The model used for scenario analyses by the group is a so-called stochastic compartmental model, in which the population is subdivided in different states or compartments, based on disease states deemed relevant to capture disease dynamics adequately [1]. More specifically, individuals are either susceptible (S), exposed but not infectious (E), infectious (I), recovered (R), or deceased (D). Moreover, individuals can also be infected with different variants of the virus and react differently to the disease, i.e., asymptomatic, mildly ill, severely ill, or getting hospitalised. Each box corresponds to a specific compartment, as illustrated in Figure 1.

Figure 1 - An illustration of the stochastic compartmental model. Each box corresponds to a compartment, S is for susceptible, E for exposed, I for infected, R for Recovered and D for deceased. Arrows represent possible transitions.

Nicolas Herman: “There are also many vaccination or immunity statuses with various vaccines and different numbers of doses, so the number of compartments can become very large.”

The stochastic aspect of the model comes from the fact that people move from one compartment to another with certain transition probabilities.

Steven Abrams: “Disease spread is intrinsically stochastic in nature with chance events, under specific conditions, either leading to a large number of new infections, or no infections at all.”

The probability of infection is related to the social contacts people have, which vary with age. Therefore, people are categorized into different age groups.

Nicolas Herman: “To model the transmission of the virus, we rely on social contact matrices, which account for social interactions in the population depending on the age of people. For example, active people more often meet other active people, children mostly contact other children, and elderly have more limited interactions.”

Fitting the Model to Real Data

This model depends on many parameters that are unknown a priori. For example, the transmission rate does not only depend on the social contact matrix (social contacts are merely a proxy for disease spread) but also on coefficients that change depending on the conditions (variant, social restrictions, seasonality, etc.), and is therefore difficult to determine. To estimate these parameters, the model must be fitted to actual data. More specifically, the modeling team used data from the CoMix survey for social contact data [2], as well as incidence data on hospitalizations and mortality, serial serological survey data (based on residual blood samples) [3] and other data sources from the COVID-19 surveillance.

Nicolas Herman: “The real difficulty is estimating the parameters. This was done using a Bayesian approach involving Markov Chain Monte Carlo (MCMC) sampling, which can take three months of computation on the Tier-2 supercomputer of the Vlaams Supercomputer Centrum.”

MCMC is a numerical method that allows for drawing values from the (posterior) distribution of unknown model parameters (including both prior information regarding these parameters and considering the data at hand), corresponding to model output that best fits the data. Despite its computational intensity, it is well-suited for estimation problems with a high number of unknown parameters.

Preparing for Future Waves…

Once the calibration is done, the model can be used to project future epidemic waves or evaluate the effectiveness of specific measures during past waves.

Nicolas Herman: “Hundreds of evaluations must be conducted for sensitivity analyses, and those can take up to 48 hours on NIC-5, the tier-2 supercomputer from ULiège. We thus used job arrays with several jobs running simultaneously.”

In the latest technical note from August 2023 [4], Nicolas Herman and his colleagues demonstrated the benefits of an early vaccination campaign in anticipation of a wave in September-October 2023. For people aged 65 or older, vaccinating people against both flu and COVID-19 significantly reduces hospital admissions for COVID-19 compared to a scenario where only 50% of the people vaccinated against the flu are also vaccinated against COVID-19 (Figure 2).

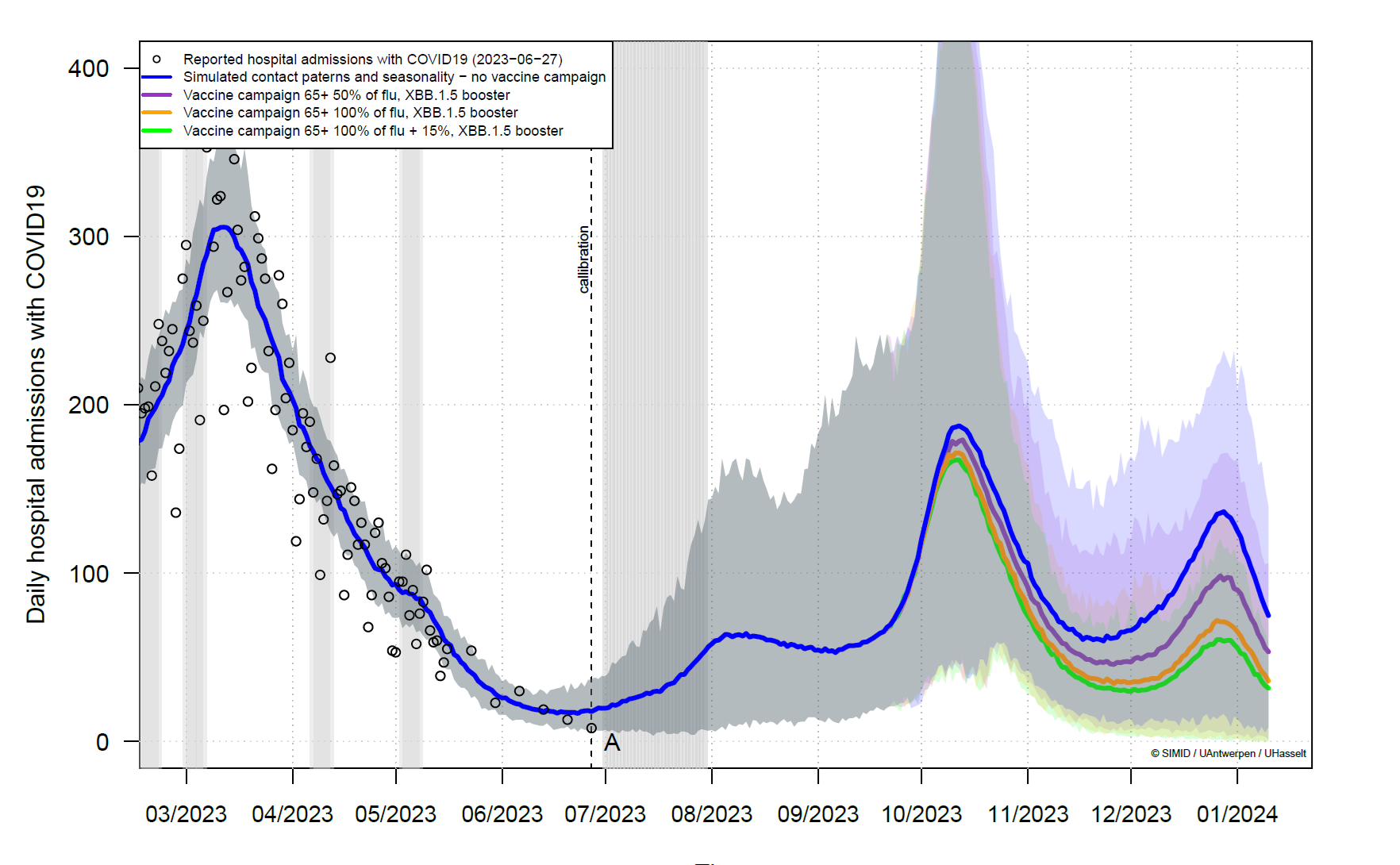
Figure 2 - Daily hospital admissions with COVID-19 in Belgium between March 2023 and January 2024. After June 2023, it corresponds to projections from the model, depending on the vaccination strategy. Taken from the technical note [4].

However, since July 2023, less data is available, and the data are less detailed because only sentinel surveillance is currently performed. The challenge for future years is to build a model that remains realistic in face of these limited data.

… and Future Pandemics!

This fruitful scientific collaboration between mathematical modelers in Flanders and Wallonia in collaboration with Sciensano has provided a firm basis for future research endeavors on pandemic preparedness. The modelling consortium also connects to the initiative taken within BE-PIN, a recently funded BELSPO project which aims at establishing a Belgian pandemic intelligence network [5].

In the long term, the goal is to extend the model to be applicable to other respiratory infections, such as flu. With this model, scientists have a powerful tool to anticipate and prepare for future pandemics.

Nicolas Herman: “The consortium aims to maintain expertise in the mathematical modeling of infectious diseases to prevent future outbreaks, within the framework of pandemic intelligence.”

Hoping it won't be necessary so soon!

[1] Willem, L., Abrams, S., Franco, N. et al. The impact of quality-adjusted life years on evaluating COVID-19 mitigation strategies: lessons from age-specific vaccination roll-out and variants of concern in Belgium (2020-2022). BMC Public Health 24, 1171 (2024). https://doi.org/10.1186/s12889-024-18576-w

[2] The CoMix survey is a survey that “follows households across Europe in real-time over the course of the COVID-19 pandemic and measures their awareness, attitudes and behaviors in response to COVID-19 and how these change over time” : https://www.uhasselt.be/en/aparte-sites-partner-en/epipose/the-comix-study

[3] Herzog, S.A., De Bie, J., Abrams, S., et al. Seroprevalence of IgG antibodies against SARS-CoV-2 – a serial prospective cross-sectional nationwide study of residual samples, Belgium, March to October 2020 (2022). Euro Surveill. 2022;27(9):pii=2100419. https://doi.org/10.2807/1560-7917.ES.2022.27.9.2100419

[4] https://covid-en-wetenschap.github.io/2023/08/technical-note-simid-august

[5] https://www.pandemicintelligence.be/